[알고리즘] 시간 복잡도를 알아보자
안녕하세요 ki입니다.
오늘은 시간 복잡도에 대해 공부하려고 합니다.
저는 프로그래머스에서 알고리즘 공부를 종종 하고 있습니다.
그중 시간복잡도에 대해 알게 됐고 그것에 대해 공부하려고 합니다.
시간복잡도(Time Complexity)
시간복잡도는 알고리즘의 효율성을 평가하는 중요한 기준 중 하나입니다. 이 기준으로 알고리즘의 실행 시간이 입력 값에 따라 어떻게 변하는지 예측할 수 있는데 예를 들어 입력 값 n이 커질 때 알고리즘이 얼마나 빠르게 실행 됐는지에 따른 결과를 분석하는 데 사용합니다.
시간복잡도 표기법
시간복잡도를 표기하기 위해 대표적인 방법은 빅오(Big-O) 표기법입니다.
빅오 표기법은 점근 표기법라고도 불리는데 빅오표기법 외에 빅 오메가 표기법(Big Omega) , 빅 세타 표기법(Big Theta) 이 있습니다. 시간복잡도를 표현하기 위해 점근표기법을 사용하는 이유로는 알고리즘에 성능을 수학적으로 표현할 수 있고, 시간복잡도와 공간복잡도를 표현하여 실제 알고리즘에 러닝타임을 보다 사용자 및 입력 값에 증가율에 따라 알고리즘에 성능을 예측하는 것을 목표로 하기 때문입니다.
표기법 종류?
- 빅오 표기법(Big-O Notation): 최초악의 실행시간 / 알고리즘 상한 / 실행시간이 선형적 증가
- 빅 오메가 표기법(Big Omega Notation, Ω\OmegaΩ): 최선의 실행시간
- 빅 세타 표기법(Big Theta Notation, Θ\ThetaΘ): 평균 실행시간 / 상한과 하한이 동일할 때 사용 / 정확한 실행시간을 표현

O(1): 입력 크기와 상관없이 항상 동일한 시간이 소요
예: 배열에서 특정 인덱스의 값을 읽는 연산. 스택에서 Push, Pop
O(n): 입력 크기에 비례하여 실행 시간이 증가.
예: 배열의 모든 요소를 하나씩 검사하는 연산. for 문
O(n^2): 입력 크기의 제곱에 비례하여 실행 시간이 증가.
예: 이중 for 문, 버블 정렬, 삽입 정렬, 선택정렬
O(2^n): 입력 크기가 증가함에 따라 실행 시간이 지수 함수 형태로 증가.
예: 피보나치수열을 재귀적으로 계산하는 알고리즘.
O(log n): 입력 크기가 증가함에 따라 실행 시간이 로그함수 형태로 증가 순차검색보다 속도 빠름
예: 이진트리
O(n log n): 입력 크기에 로그를 곱한 형태로 실행 시간이 증가하는 경우.
예: 퀵정렬, 병합정렬, 힙정렬
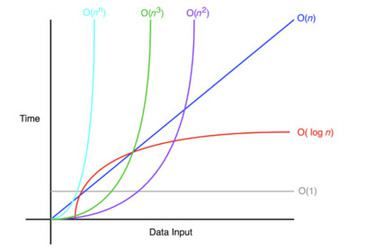
* 성능 비교 ( 우측으로 갈수록 빠름)
O(1)<O(logn)<O(n)<O(nlogn)<O(n2)<O(n3)<O(2n)
예제별 코드로 구현
// O(1) 입력 크기와 상관없이 항상 동일한 시간이 소요되는 경우
// 데이터가 증감함에 따라 성능의 변함 없음
F(int [] n ) {
return (n[0] == 0 ) ? true:false;
}
// O(n)
// n이 1씩 늘어날때마다 처리시간이 증가함
F(int[] n) {
for i = o to n.length
print i;
}
// O(n^2)
// 두 번 실행해서 면적처럼 나타낼수 있음
F(int[] n) {
for i = 0 to n.length
for j = 0 to n.length
print i+j;
}
// O(nm)
F(int []n , int[]m ) {
for i = o to n.length
for j = o to m.length
print i + j;
}
// O(n^3)
// 데이터가 큐빅모양을 형태가 보임
F(int [] n) {
for i = 0 to n.length
for j = 0 to n.length
for k = 0 to n.length
print i+j+k;
}
// O(2^n)
// 바로 전 숫자와 전전숫자를 알아야함 더할 수있음
F(n,r) {
if (n ≤ 0) return 0 ;
else if ( n ==1 ) retrun r[n] = 1;
return r[n] = F(n-1,r) +F(n-2 , r) ;
}
// O(m^n) : 2에 ^n 에서 2를 m으로만 바꿔주면 됨
// O(log n)
F(k,arr,s,e) {
if (s > e) return -1;
m=(s+e) /2;
if( arr[m] == k ) return m;
else if (arr[m] > k) return F(k,arr,s,m-1);
else return F(k,arr,m+1,e);
}
빅오 vs 빅오메가 vs 빅세타에서 빅오를 사용하는 이유
- 최악의 경우 : 가장 극단적인 상황에서 알고리즘의 성능을 예상할 수 있어 안정성과 신뢰성을 보장하는 데 유용합니다
- 단순함과 명확성 : 복잡한 상수를 모두 숫자는 1로 설정하여 크기에 따른 영향을 미치는 부분만을 고려하고 이해하기 쉬워 알고리즘을 비교하고 분석하는 데 매우 유용합니다. 따라 알고리즘의 실행 시간을 간결하고 명확하게 표현합니다.
- 알고리즘 간의 비교 : 다양한 알고리즘의 시간복잡도를 쉽게 비교할 수 있습니다.
마무리
코드 작성 시 시간복잡도를 고려해야 하는 이유는 효율적인 코드를 작성하고 시스템 성능을 최적화하며 문제 해결 능력을 향상하는 데 매우 중요하다는 것입니다.!